HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG | Bài toán nâng cao hình học 9

9/14/2023 3:48:27 PM

phamanhq ...

A. KIẾN THỨC CƠ BẢN

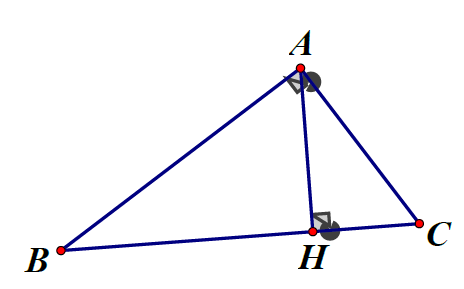
Cạnh huyền BC
Cạnh góc vuông AB, có hình chiếu lên cạnh huyền là BH
Cạnh góc vuông AC , có hình chiếu lên cạnh huyền là CH. Đường cao AH.

BC²= AB²+ AC²

Trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông

AB² = BC.BH

AC² = BC.CH

Trong tam giác vuông, bình phương độ dài mỗi cạnh góc vuông bằng tích độ dài cạnh huyền với hình chiếu của cạnh góc vuông đó lên cạnh huyền

AH² = BH.CH

Trong tam giác vuông, bình phương độ dài đường cao ứng với cạnh huyền bằng tích độ dài hình chiếu của hai cạnh góc vuông lên cạnh huyền.

$\frac{1}{AH^{2}}=\frac{1}{AB^{2}}+\frac{1}{AC^{2}}$

Trong tam giác vuông, nghịch đảo bình phương độ dài đường cao bằng tổng nghịch đảo bình phương độ dài hai cạnh góc vuông.

AB.AC = BC.AH

Trong tam giác vuông, tích độ dài hai cạnh góc vuông bằng tích độ dài cạnh huyền với đường cao tương ứng.

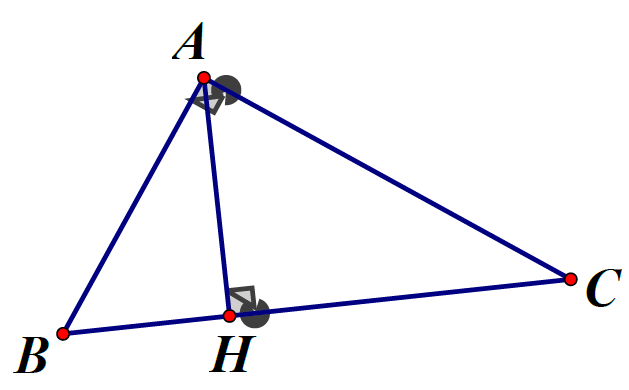
Ví dụ 1:Cho tam giác ABC vuông tại A, đường cao AH . Biết AB : AC = 3: 4 và AB + AC = 21cm.

a) Tính các cạnh của tam giác ABC

b) Tính độ dài các đoạn AH,BH,CH

Giải:

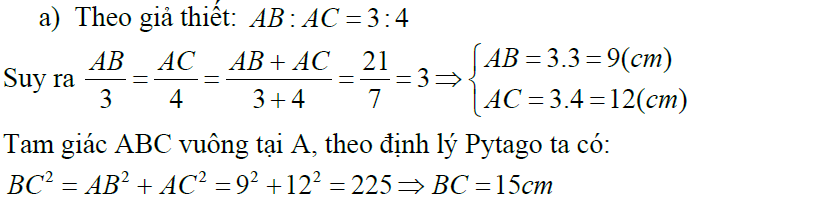
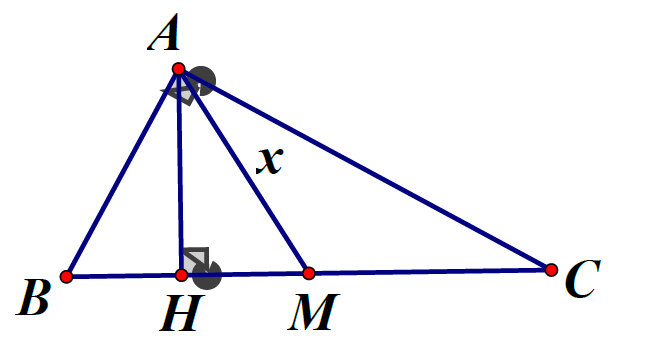
Ví dụ 2:Tính diện tích một tam giác vuông có chu vi 72 cm, hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng 7 cm.

Giải:

File bài tập (Cuối bài viết)